Analog Voronoi Grid Distortion with Magnets

Using a magnetically distorted grid of washers as input sites for the Voronoi diagram.



(See also: How to: Draw the Voronoi Diagram)

2009-09-20 21.01.44.jpg

2009-09-20 21.01.44.jpg, originally uploaded by sevensixfive.

How to: Draw the Voronoi Diagram

As has been written here before, Voronoi diagrams, as a geometric model are fascinating because they can be used to describe almost literally everything: from cell phone networks to radiolaria, at every scale: from quantum foam to cosmic foam. Even the regular lattices and solids, cubes, tetrahedra, and the ways in which they combine, can all be seen as special cases of three dimensional Voronoi. It's hard not to get mystical about it, but it's really just the contemporary equivalent of the endless ideal gridded space of modernism or the renaissance, just more exotic and malleable. Geometry is Culture.

Drawing Voronoi diagrams by hand has renewed my interest in the stuff. There are lots of scripts out there for making instant vector crystal foam in just about any modeling or CAD platform, but it's more interesting for me right now to slow it down, take it step by step, and really try to understand the geometries involved. More a heuristic than an algorithm, executing it demands and reinforces the kind of zoned out close attention that almost becomes the whole point of drawing in the first place. The artifact that you get at the end it is just an unexpected bonus: the physical record left by the process of thinking out loud on paper. Below is a rough pseudocode (thanks, mike!) for building it up from a set of points.


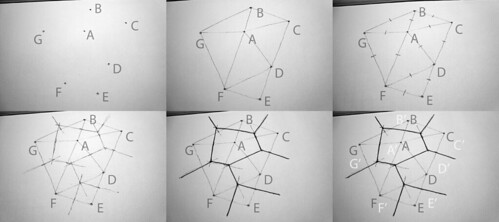(1) Input Sites (2) Connect Nearest Neighbors (shortest line wins) (3) Find Center Points
(4) Draw Perpendicular Bisectors (5) Trace Cells (6) voila

(1) The input points, step one, are called sites, labeled here A, B, C, etc.

(2) The next step is to connect the sites to all of their nearest neighbors without making a line that crosses another. This is known technically as the Delauney Triangulation, and it's maybe the most difficult part. One way to do it might be by brute force - connect every site to every other site, make a true all-to-all rhizomatic meshwork, and then start deleting lines that are too long. This is how a machine might attack the problem, but it becomes too hard for a human to execute when the number of sites jumps into the double digits. Another algorithmic method is to start with a test triangle of sites and draw their circumcircle, the circle that hits all three sites, rejecting the triangle if the circle contains another site within it.


Image via wikipedia

This also takes too long, and circumcircles are hard to draw, so I found a method that's faster, and still mostly accurate. Since no lines on the Delauney triangulation can cross, just eyeball it until you run into a condition as in the above, where you have to decide if FD or AE is correct, the shorter line always wins. This is obvious in the example, but sometimes this needs some careful measuring in the field.

(3) Step three is to find and mark the centerpoint of every line on the Delauney graph.

(4) The fourth step is to draw the perpendicular bisector for each Delauney line. This is where careful accuracy, in finding the centerpoints, and in drawing a tight 90 degree angle, pays off. If everything has been done correctly, there will always be three lines converging at a point, unless the input sites are on a perfectly regular rectangular grid. Drawing the last line of the three and watching it land exactly where it's supposed to is extremely satisfying. Watching it miss can mean going back all the way to step two and flipping the Delauney graph for the triangle. Some mistakes are instructive, reminding you to take your time and think about the moves, but some are more interesting, for being completely inexplicable. A few places in these drawings, I've run into conditions that should work out, but just don't: evidence of some hidden monster in the process, a flaw in the heuristic, or a breakdown of the pseudocode.

(5) The fifth step is to retrace the outline of each Voronoi cell from the perpendicular bisectors. There will be one cell for every site, and at the end, each cell is just the set of all surface area points that are closer to its site than any of the other sites, as illustrated in the last panel: A' -> A, B' -> B, etc.

(6) Sit back and congratulate yourself while contemplating your hard earned tangle of fat distorted honeycomb.



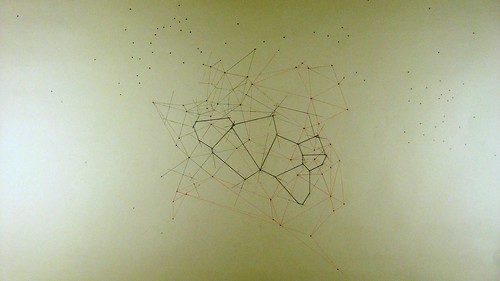
I've found in practice that it's best to use different colors for the input sites, the Delauney lines, and the bisectors, unless driving yourself completely crosseyed mad is something you have the time and inclination to do. Blue and red mechanical pencil leads are pretty easy to get. I made this drawing to practice, using a pepper grinder above the drafting table to get random input sites:



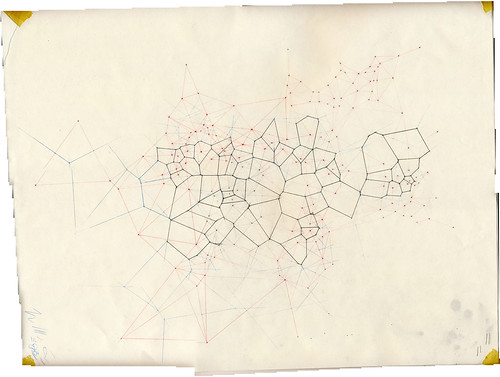
The wall drawing below was made for the Current Gallery's Abandon Ship show. It measures about 3' x 5'. The input sites here were the roughly patched holes and marks left by all the previous exhibits and shows in the space's three year existence as a gallery. Before that, the building was a chocolate factory. This piece will be demolished along with the rest of the show when (if) plans move ahead to build a hotel on the site. I was very glad to get the chance to do a wall drawing, having just visited again, for the second time, Sol LeWitt's ephemeral 'Drawing Series—Composite, Part I–IV, #1–24, A+B' at Dia Beacon. These pieces foreground the disconnect and shifts between the different types of time at play here: the almost instantaneous time of conception, the time spent to absorb the system, process the clues, unlock and understand the method, and the implied slow time spent to execute the drawing itself: a person, on a scaffold, pulling graphite repeatedly across painted gypsum. I wonder if the assistants were well paid.



The five hours or so it took to carry out the Current Gallery piece were well spent: not an all nighter, but a late nighter. Friends brought food and beer, with other people coming and going, cutting holes in the building's floor, plastering the backside with xeroxed drawings, and making Seussian maggots crawl from the walls and ceiling.

[[Edit: If anyone else has tried this, put some pics of it on the web and post a link in the comments]]

[[[Edit 2: for more, see also: Analog Voronoi Grid Distortion with Magnets]]]